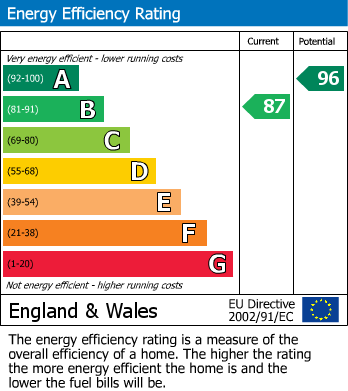
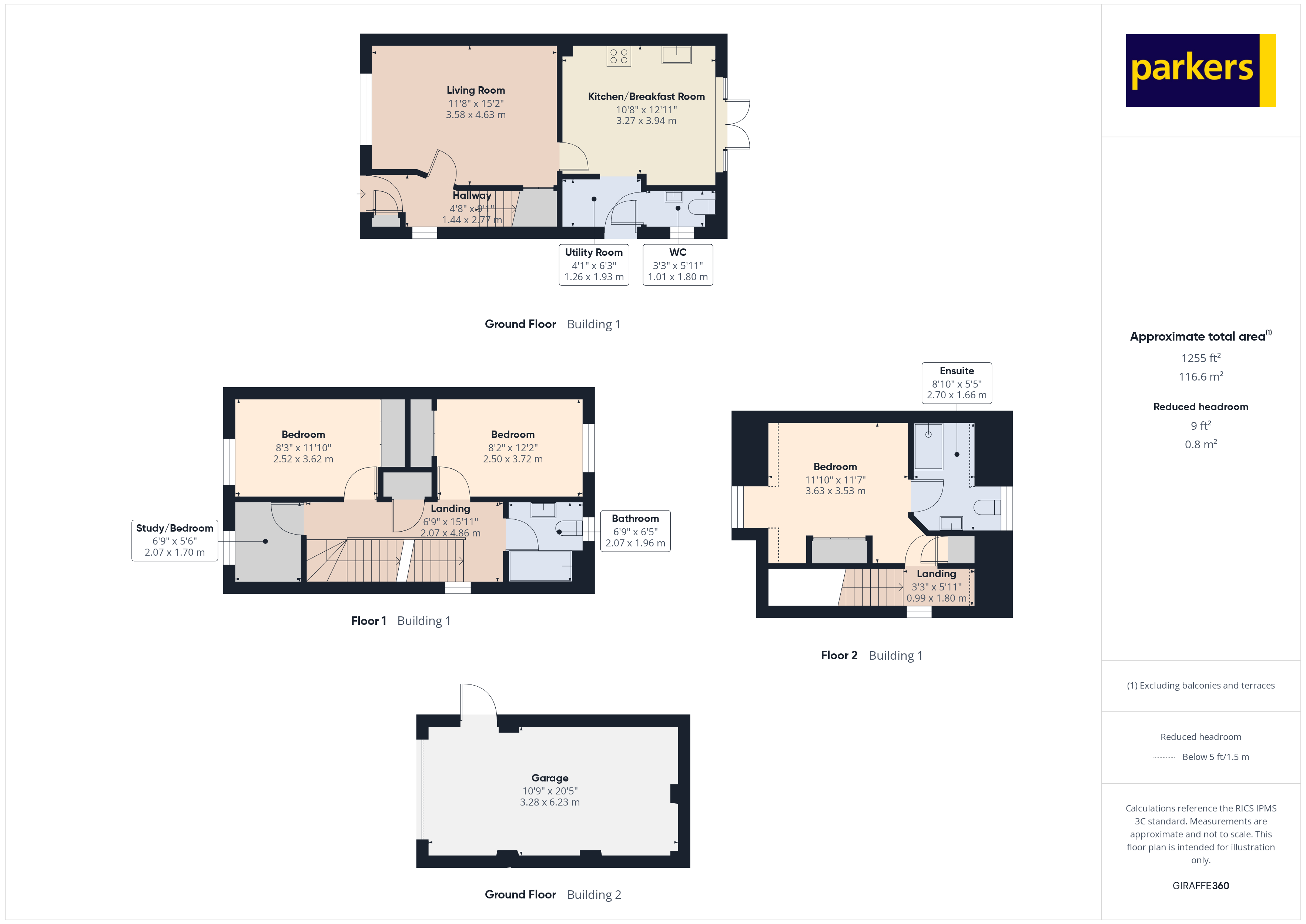
- Living room
- Kitchen/breakfast room
- Utility room
- Downstairs cloakroom
- Master bedroom with ensuite
- Three further bedrooms
- Family bathroom
- Garage and driveway parking
Set within an exclusive development in Greenham, this beautifully presented three/four-bedroom semi-detached townhouse offers versatile accommodation and an enviable location, with Newbury Retail Park and the open spaces of Greenham Common just moments away. Inside, the property boasts a spacious living room to the front, leading seamlessly into a stylish kitchen/dining area complete with modern fitted appliances and patio doors opening onto the rear garden — perfect for entertaining. A separate utility space and downstairs cloakroom add further practicality. The first floor offers two generous double bedrooms both with fitted wardrobes served by a contemporary family bathroom, along with a third smaller bedroom, ideal as a home office or study. On the top floor, the impressive principal suite features fitted wardrobes and a private ensuite shower room, providing the perfect retreat. Outside, the property benefits from driveway parking and a detached garage with power and lighting, as well as side gated access and a rear garden door into the garage for added convenience. This superb home combines modern living with a highly sought-after location, making it an excellent choice for families and professionals alike. • Closest train station: o Newbury station — approximately 0.9 miles away o Newbury Racecourse station — approximately 1.2 miles away • Closest primary school: o Fir Tree Primary School and Nursery — approximately 0.5 miles away • Closest secondary school: o Trinity School — approximately 1.4 miles away These particulars are a general guide only. They do not form part of any contract. Services, systems and appliances have not been tested. The title is currently under review for any potential covenants or restrictions.
| Tax Band | % | Taxable Sum | Tax |
|---|
Struggling to find a property? Get in touch and we'll help you find your ideal property.